An estimation of cost and substitution effects on the price of benzene
A formal model for solving the problem
Published by Edoardo Pace. .
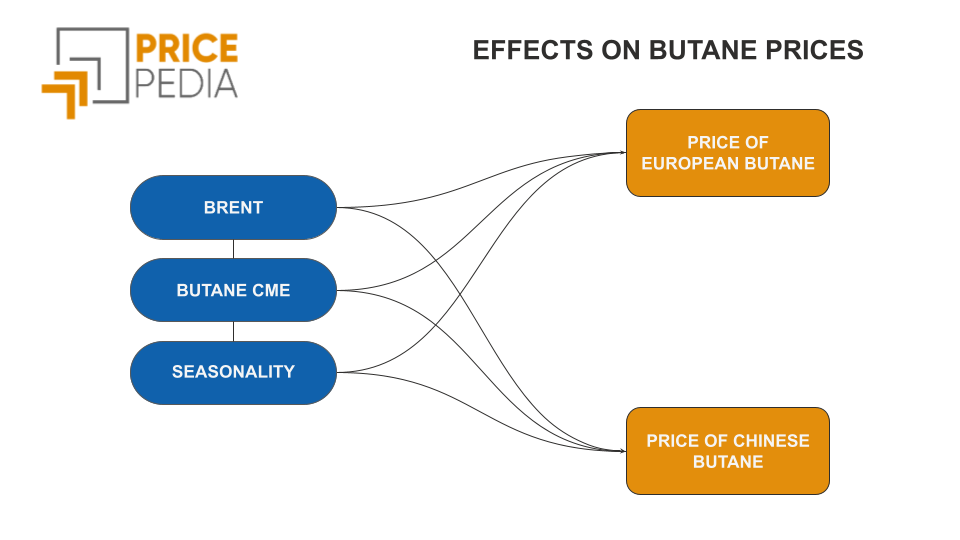
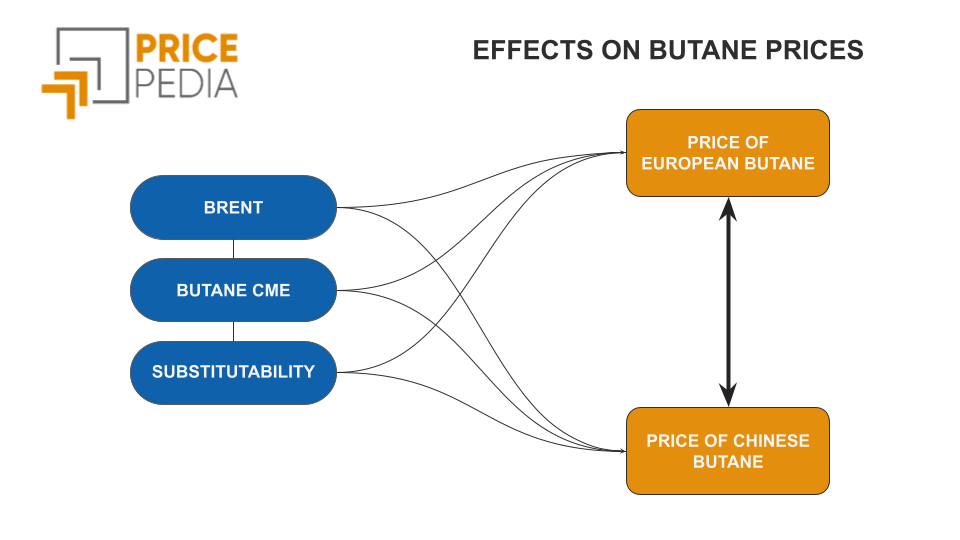
Organic Chemicals Analysis tools and methodologiesUnderstanding the mechanisms behind commodity price formation is essential for analyzing market dynamics and the behavior of economic agents. The case of benzene, produced through different manufacturing technologies, offers an interesting opportunity for further exploration. Benzene can be produced via two distinct industrial processes: in the first, it is derived using naphtha[1]; in the second, it is obtained from coal tar. The two types of benzene are strong substitutes, as evidenced by the close correlation in their respective price trends.
Comparison between benzene from naphtha and benzene from coal tar prices

The chart shows that, in the long run, there is a strong relationship between the two series, with the price of benzene from naphtha on average 30% higher than the price of its substitute.
Determinants of benzene price
Based on the microeconomic approach of market equilibrium, the price of benzene is mainly determined by:
- Its production costs;
- Demand and supply tensions in the market.
In the long run, it is demonstrable that, for each type of benzene, there is a stable relationship between price and a combination of production costs and market tensions.
We will refer to these relationships as “cost relationships” in the long run, since cost components generally represent the main determinant of the final benzene price.
In addition to the cost relationship, the two benzene prices are linked by a long run “substitution relationship”, as shown by the strong alignment of the two price series over time.
One way to account for both relationships is to consider their respective long-run equations and include both adjustment mechanisms— cost-related and substitution-related — in the short-run equations. This way, the model can represent both cost and substitution relationships, allowing for more accurate forecasting.
Error Correction Models
The model developed is an Error Correction Model (ECM) built using an economic approach. According to this approach, the ECM can be divided into two parts:
- A part containing the long-run equations derived from the respective relationships;
- A part gathering the short-run equations, which reflect both the shock effects from changes in the long-run levels and the ECM adjustment mechanisms related to past values.
Long-run equations
For each benzene type, two long-run relationships can be defined: in the first (cost), the price level is assumed to be determined by the cost of production factors — naphtha (N) or coal tar (C) — the Consumer Price Index (CPI, i.e., inflation), and the Industrial Cycle Index (IC); in the second (substitution), the price of one benzene is a function of the price of its substitute.
So, the long-term equations identified are:
For benzene from naphtha (B):
For benzene from coal tar (BC):
All parameters in the equations have been estimated using OLS and are kept fixed in the dynamic phase that follows.[2]
Short-run equilibrium (ECM phase)
In the short-run equations, the variation in benzene prices is determined by:
- The variation in its long-run level, itself influenced by changes in structural determinants;
- An error correction component related to the long-run cost relationship;
- An error correction component related to the long-run substitution relationship.
For benzene from naphtha, the estimated equation is:
While. for benzene from coal tar:
Consequently, the model captures price adjustments in response to:
- Shocks in the costs of production factors;
- Macroeconomic conditions, represented by inflation and industrial cycle;
- Shocks in the substitute product’s price;
- Deviations from the long-run cost equilibrium;
- Long-run substitution effects between the two final products.
The economic meaning of the parameters is as follows:
- \( \gamma_1 \) and \( \gamma'_1 \): price elasticity of each benzene to changes in costs (input and macroeconomic conditions);
- \( \gamma_2 \) and \( \gamma'_2 \): speed of adjustment toward the long-run cost equilibrium;
- \( \gamma_3 \) and \( \gamma'_3 \): price elasticity to the change in the substitute’s price;
- \( \gamma_4 \) and \( \gamma'_4 \): speed of adjustment toward the long-run substitution equilibrium.
Estimation results
Long-run equations
In the case of benzene, all the model’s long-run relationships are found to be cointegrated. This allows each equation to be estimated separately using the OLS estimator. The table below reports the estimated parameters.
Estimated parameters for the long-run cost relationship (*)
| Benzene | Raw material (\( \beta_1 \)) | Inflation (\( \beta_2 \)) | Industrial cycle (\( \beta_3 \)) |
|---|---|---|---|
| from naphtha | 0.808 | 0.244 | 0.606 |
| from coal tar | 0.376 | 0.577 | 2.265 |
(*) All reported parameters are statistically significant
Estimated parameters for the long-run substitution relationship (*)
| Benzene | Substitute (\(S_0 \)) |
|---|---|
| from naphtha | 0.871 |
| from coal tar | 1.026 |
(*) All reported parameters are statistically significant
Then, the long-run coefficients were inserted into the short-run equations to estimate the four short-run parameters described above, again using OLS.
Short-run equations
Subsequently, the short-term estimation results were calculated by considering only the cost dynamics, and the residuals from this regression were saved. These same residuals were then used as the dependent variable in the second short-term estimation, which included only the substitution dynamics.
It was necessary to use this two-step method due to multicollinearity issues encountered in the case of a single-equation estimation. Therefore, the results presented below may not be entirely statistically optimal, but they are at least consistent with the economic facts.
The results are shown in the following table:
Estimated parameters for the short-run relationship
| Benzene | Cost shock (\( \gamma_1 \)) | Cost ECM (\( \gamma_2 \)) | Substitution shock (\( \gamma_3 \)) | Substitution ECM (\( \gamma_4 \)) |
|---|---|---|---|---|
| from naphtha | 0.485 | 0.404 | 0.425 | 0.312 |
| from coal tar | 0.704 | 0.154 | 0.475 | 0.599 |
Implications of the short-run results
For naphtha-based benzene, in the first phase, cost factors are fully relevant: both the shock (\( \gamma_1 = 0{.}485 \)) and the error correction term (\( \gamma_2 = 0{.}404 \)) are significant and positive, indicating that variations in input costs and deviations from the cost equilibrium directly and consistently affect the price of naphtha-based benzene. In the second phase, the component related to the substitute benzene also proves significant: the price of coal tar benzene generates an immediate effect (\( \gamma_3 = 0{.}425 \)) and an adjustment toward the substitution equilibrium (\( \gamma_4 = 0{.}312 \)), albeit with a lower intensity compared to the cost component.
For coal tar-based benzene, similar dynamics emerge but with a different relative weight between the two components. The cost part shows significant coefficients for both terms: the shock (\( \gamma'_1 = 0{.}704 \)) and the error correction term (\( \gamma'_2 = 0{.}154 \)) indicate an important role of costs in determining the short-term price. The substitution component displays higher coefficients: the shock (\( \gamma'_3 = 0{.}475 \)) and the adjustment toward the substitution equilibrium (\( \gamma'_4 = 0{.}599 \)) are both significant and denote a high sensitivity of the coal tar benzene price to variations in the price of naphtha-based benzene.
Overall, the two-step approach made it possible to obtain estimates more consistent with economic theory, highlighting how both factors — costs and substitution — contribute to price determination, with a particularly strong role of substitution in the case of coal tar benzene and a more balanced contribution for naphtha-based benzene, consistent with the fact that benzene production is dominated by that produced from naphtha.
In conclusion
The adoption of the two-step procedure made it possible to more effectively isolate the impact of cost factors and substitution dynamics on benzene prices. The results confirm that, although the substitution links between naphtha-based and coal tar-based benzene represent a crucial channel for the transmission of price variations, production costs and macroeconomic conditions also play a significant role, particularly for naphtha-based benzene.
Do you want to stay up-to-date on commodity market trends?
Sign up for PricePedia newsletter: it's free!
[1] For a more detailed analysis of the relationship between the two types of benzene, see: [2] All variables have been considered in logarithms. This way, the estimated parameters can be interpreted as "elasticities."